JAX, ovvero NumPy sotto steroidi

8 minute read

⚠️ Il post che segue è un backup dell’articolo originale, pubblicato a fine 2018 sul blog della (ormai defunta) Italian Association for Machine Learning. Il post è stato mantenuto senza modifiche per ragioni ‘storiche’, ma la maggior parte delle informazioni rimangono corrette.

Nell’era dei ‘giganti’ (TensorFlow, PyTorch, …), introdurre e studiare una nuova libreria di machine learning potrebbe sembrare controproducente. Eppure JAX, un nuovissimo progetto di ricerca targato Google, ha diverse caratteristiche che lo rendono di interesse ad un vasto pubblico. In primo luogo, si presenta come un vero e proprio wrapper di NumPy, rendendo la transizione da quest’ultima libreria quasi immediata. In secondo luogo, fa dell’efficienza uno dei suoi punti di forza, grazie all’uso trasparente di XLA, un acceleratore di algebra lineare originariamente sviluppato per TensorFlow. Infine, ed è forse la novità più intrigante, è una delle prime librerie a puntare fortemente su una anima di pura programmazione funzionale.

JAX - A confronto con i giganti

Fondamentalmente, ogni libreria di reti neurali in commercio si può categorizzare sulle base di quattro elementi chiave:

  1. Il modo in cui permette di esprimere e manipolare operazioni su tensori (es., grafi computazionali vs. esecuzione eager);
  2. Strumenti e modalità di differenziazione automatica (es., possibilità di avere gradienti di ordine superiore);
  3. Le tecniche che mette a disposizione per accelerare il codice su GPU, sistemi distribuiti, o altro;
  4. I moduli ad alto livello eventualmente presenti per costruire ed allenare le reti neurali stesse.

Questi quattro punti permettono una enorme differenziazione nell’ecosistema: Keras, ad esempio, si è originariamente affermata puntando quasi tutto sul punto (4), lasciando ad un backend a scelta gli altri compiti. Autograd, invece, nel 2015 puntò sui primi due punti, permettendo di scrivere codice usando solo costrutti “classici” di Python e NumPy, fornendo poi tantissime opzioni per il secondo punto. La semplicità di Autograd influenzò moltissimo lo sviluppo delle librerie a seguire, ma essa fu penalizzata dalla netta carenza dei punti (3) e (4), ovvero tecniche adeguate per accelerare il codice e sviluppare ad alto livello.

JAX è, fondamentalmente, la versione 2.0 di Autograd: ne riprende l’intera filosofia, aumentandola con diverse tecniche di accelerazione su GPU/TPU e con piccole librerie ad alto livello per la prototipazione di modelli e la loro ottimizzazione. Può quindi essere di enorme interesse per diverse fasce di utenti: per chi volesse solo accelerare codice NumPy, o per chi ama sviluppare “dal basso” senza spostarsi troppo dalla familiarità di NumPy. Ed infine, punto non da poco, per chi cercasse una libreria dall’animo puramente funzionale.

Nel resto di questo articolo vediamo rapidamente le funzionalità principali di JAX disponibili al momento (versione 0.12), seguendo parti del tutorial originario ed estendendole quando necessario.

Tutto il codice di questo articolo è disponibile su un notebook Google Colab.

Installare JAX

Installare JAX richiede di compilare XLA sulla propria architettura, seguendo le istruzioni sul sito. Su Google Colab trovate una versione binaria già pronta che potete installare molto facilmente:

!pip install --upgrade https://storage.googleapis.com/jax-wheels/cuda92/jaxlib-0.1.2-py3-none-linux_x86_64.whl

!pip install --upgrade jax

Il resto del tutorial presuppone questo setup.

JAX core 1: il wrapper NumPy

Cominciamo dalle basi: un po’ di istruzioni a caso di NumPy.

import numpy as np

x = np.ones((5000, 5000))
y = np.arange(5000)

z = np.sin(x) + np.cos(y)

Il codice equivalente di JAX richiede solo di importare il wrapper apposito per NumPy:

import jax.numpy as np # Unica differenza!

x = np.ones((5000, 5000))
y = np.arange(5000)

z = np.sin(x) + np.cos(y)

Già così l’utilizzo di XLA ci garantisce una buona accelerazione: sul backend GPU di Colab, il codice di prima gira in 30 ms contro circa 480 ms del codice NumPy. Non tutte le funzioni di NumPy/SciPy sono ancora implementate, ma dovrebbero esserlo a regime della libreria. Se oltre ad accelerare codice volete usare anche tutte le funzionalità che seguono (es., auto-differenziazione), allora ci sono alcuni vincoli aggiuntivi sul codice che potete scrivere, derivanti anche dalla natura funzionale della libreria: ad esempio, non potete modificare i valori di un array tramite indicizzazione.

JAX core 2: il compilatore JIT

Il codice di prima accelera ogni istruzione tramite XLA, ma in generale potreste voler accelerare interi blocchi di codice sfruttando eventuali parallelismi al loro interno. In questo caso, JAX mette a disposizione un meccanismo di compilazione tramite tracing molto simile al compilatore JIT di PyTorch.

Il funzionamento è molto semplice, possiamo usare un’annotazione (od una funzione esplicita) per indicare a JAX cosa compilare:

from jax import jit

@jit
def fn(x, y):
  z = np.sin(x)
  w = np.cos(y)
  return z + w
 
# Alternativa senza annotazione:
# fn = jit(fn)

In questo caso JAX compilerà la funzione al suo primo utilizzo, riusando la versione ottimizzata successivamente. Sul backend GPU di Colab otteniamo un ulteriore guadagno del 30% circa, riducendo il tempo medio di esecuzione a 20 ms. L’utilizzo del compilatore richiede però qualche vincolo aggiuntivo, in particolare sull’indicizzamento e le istruzioni condizionali e di flusso.

JAX medium 1: auto-differenziazione

Il meccanismo di auto-differenziazione è simile a quello presente in altre librerie: data una funzione Python con una serie di manipolazioni su tensori, possiamo automaticamente ottenerne una seconda che ne calcola il gradiente in maniera automatica:

from jax import grad

@jit
def simple_fun(x):
  return np.sin(x) / x

# Ritorna il gradiente di simple_fun rispetto ad x  
grad_simple_fun = grad(simple_fun)

Possiamo concatenare più chiamate per ottenere gradienti di ordine superiore:

# Calcola la seconda derivata (diagonale dell'Hessiana)
grad_grad_simple_fun = grad(grad(simple_fun))

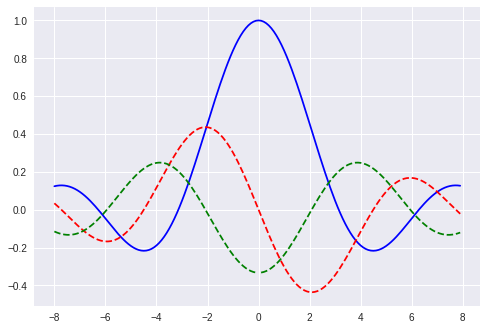
Possiamo graficare il tutto!

import matplotlib.pyplot as plt
plt.plot(x_range, simple_fun(x_range), 'b')
plt.plot(x_range, [grad_simple_fun(xi) for xi in x_range], '--r')
plt.plot(x_range, [grad_grad_simple_fun(xi) for xi in x_range], '--g')
plt.show()

JAX medium 2: vettorizzazione avanzata con vmap

Oltre ad accelerare ogni singola istruzione, ed al tracer, JAX mette a disposizione un terzo meccanismo di accelerazione, da usare quando vogliamo applicare la stessa funzione su uno o più assi di un tensore. Vediamo un esempio pratico riprendendo il calcolo del gradiente di prima:

# Calcolo del gradiente (naive)
[grad_simple_fun(xi) for xi in x_range]

Come in molte librerie, JAX suppone che la funzione che state differenziando abbia un solo output. Per calcolare più gradienti in parallelo, in questa situazione abbiamo dovuto richiamarla separatamente per ogni valore. Possiamo ottenere lo stesso effetto con una chiamata all’operatore vmap:

from jax import vmap
grad_vect_simple_fun = vmap(grad_simple_fun)(x_range)

vmap restituisce una nuova funzione che applica la funzione originaria (grad_simple_fun) su un intero vettore. In questo semplice modo, otteniamo uno speedup di 100x sull’esecuzione (4 ms contro 400 ms)!

In generale, grad, jit e vmap sono tre esempi di quelle che JAX chiama trasformazioni componibili, ovvero operatori applicabili ad una generica funzione, e componibili fra loro.

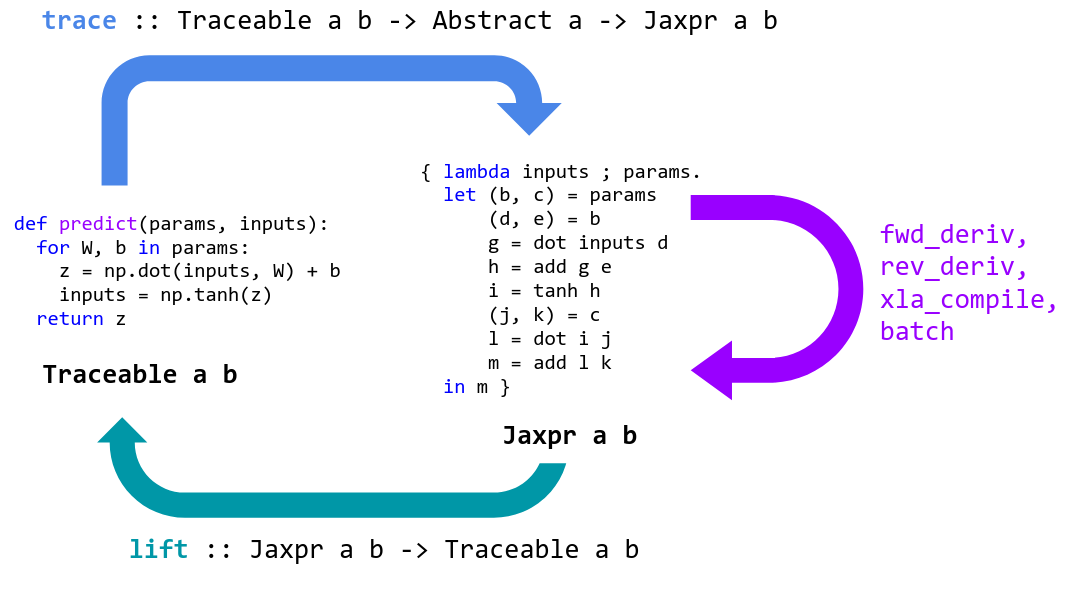JAX lifecycle Schematizzazione del “ciclo di vita” di una funzione in JAX. Fonte: JAX GitHub.

JAX core 2.5: generazione di numeri pseudocasuali

Prima di passare a vedere alcuni costrutti di alto livello per l’allenamento di reti neurali, è necessario discutere brevemente del modo in cui JAX gestisce i numeri pseudocasuali. JAX implementa un proprio PRNG che, a differenza di quello NumPy, ha un’interfaccia puramente funzionale, ovvero senza side effects: tra le altre cose, una chiamata ad un metodo pseudocasuale (es., randn) non può modificare lo stato interno del generatore.

Per questo, gli utenti in JAX devono esplicitamente richiamare e manipolare lo stato del PRNG, nella forma di una chiave:

from jax import random

# Genera una chiave
key = random.PRNGKey(0)

# La chiave va passata esplicitamente durante la creazione di un array di numeri pseudocasuali
print(random.normal(key, shape=(3,)))

Differenza essenziale, come detto, è che la chiave non viene modificata dalla chiamata a random.normal: chiamate successive alla funzione con la stessa chiave produrrebbero array uguali. Per modificare la chiave, dobbiamo ‘sdoppiarla’ con una chiamata apposita:

# Ottiene due chiavi separate
key, new_key = random.split(key)

# Usando due chiavi diverse, abbiamo risultati diversi
print(random.normal(key, shape=(3,)))
print(random.normal(new_key, shape=(3,)))

Questo è forse l’aspetto meno intuitivo e più prono ad errori della libreria allo stato attuale, e potrebbe essere modificato / migliorato in futuro.

JAX advanced 1: costruire reti neurali con STAX

JAX contiene al suo interno anche delle mini-librerie che ne mostrano le potenzialità. Una di queste, STAX, è dedicata a costruire reti neurali, con un’interfaccia simile ad altri framework di deep learning. Ad esempio, possiamo costruire una rete come “stack” di diversi “strati”:

from jax.experimental import stax
from jax.experimental.stax import Dense, Relu, LogSoftmax

net_init, net_apply = stax.serial(
    Dense(10), Relu,
    Dense(3), LogSoftmax,
)

A differenza di altri framework, però, la rete neurale così ottenuta rispetta un’interfaccia funzionale e non ad oggetti: in particolare, la rete è definita da una coppia di funzioni, rispettivamente per l’inizializzazione dei parametri e la predizione.

# Inizializza la rete con quattro input
out_shape, net_params = net_init((-1, 4))

# Ottiene le predizioni della rete
print(net_apply(net_params, Xtrain))

JAX advanced 2: ottimizzazione con minmax

La seconda libreria di JAX, minmax, permette invece di ottimizzare funzioni costo. Supponiamo di definire una funzione di costo per la nostra rete (es., cross-entropia):

def loss(params):
  predictions = net_apply(params, Xtrain)
  return - np.mean(ytrain * predictions)

All’interno di minmax troviamo diversi algoritmi già implementati, tra cui Adam:

from jax.experimental import minmax
opt_init, opt_update = minmax.adam(step_size=0.01)

Anche l’ottimizzatore, come la rete neurale, non è ad oggetti ma è definito da due funzioni, una per l’inizializzazione ed una per il passo di aggiornamento (dati i gradienti). Vediamo il codice per un singolo passo di ottimizzazione:

@jit
def step(i, opt_state):
  # Parametri dell'algoritmo di ottimizzazione
  params = minmax.get_params(opt_state)
  # Gradienti della funzione costo
  g = grad(loss)(params)
  # Passo di aggiornamento
  return opt_update(i, g, opt_state)

Ed il codice complessivo dell’ottimizzazione:

# Inizializzazione dell'ottimizzatore
opt_state = opt_init(net_params)
for i in range(100):
  opt_state = step(i, opt_state)
# Parametri finali dopo l'allenamento
net_params = minmax.get_params(opt_state)

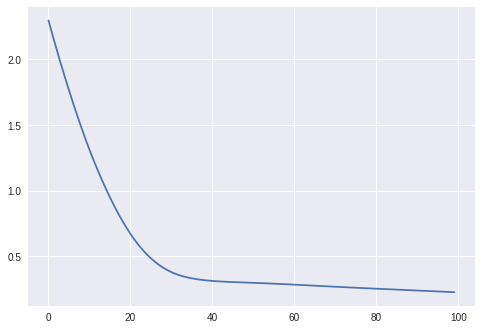
minmax permette di ottimizzare funzioni costo nelle quali i tensori sono definiti all’interno di liste o dizionari in maniera completamente trasparente: l’importante è che i gradienti passati alla funzione di update rispettino lo stesso formato.

Ricapitolando

JAX è una libreria molto giovane ma molto promettente per un vasto pubblico, sia che decida di implementare dal basso sfruttando la forte accelerazione della libreria, sia che si senta ispirato dalla sua interfaccia fondamentalmente funzionale. In attesa del rilascio della prima versione stabile, speriamo che questo breve tutorial vi abbia stuzzicato l’interesse!